Программа

факультатива по математике 5 класса

Учитель математики:  Вальченко Н.В.  

2013-2014 уч. год.

ВВЕДЕНИЕ.

         Факультативные занятия по математике в 5 классе являются одной из важных составляющих программы «Работа с одаренными детьми».

На первых этапах проведения занятий определена цель – показать учащимся красоту и занимательность предмета, выходя за рамки обычного школьного учебника. В дальнейшем ставятся цели, наиболее актуальные сегодня при переходе к профильному обучению.

Факультативный курс направлен на достижение следующих целей:

• развитие логического мышления;
• раскрытие творческих способностей ребенка;
• воспитание твердости в пути достижения цели (решения той или иной задачи);
• привитие интереса к предмету.

Кроме того, факультативные занятия решают такие актуальные на сегодняшний день задачи, как:

• адаптация учащихся при переходе из начальной школы в среднее звено;
• работа с одаренными детьми в рамках подготовки к предметным олимпиадам и конкурсам.

При разработке факультативного курса по математике учитывалась программа по данному предмету, но основными все же являются вопросы, не входящие в школьный курс обучения. Именно этот фактор является значимым при дальнейшей работе с одаренными детьми, подготовке их к олимпиадам различного уровня.

ПОЯСНИТЕЛЬНАЯ  ЗАПИСКА

Программа факультативного курса по математике для учащихся 5 классов направлена на расширение и углубление знаний по предмету. Темы программы непосредственно примыкают к основному курсу математики 5 класса. Однако в результате занятий учащиеся должны приобрести навыки и умения решать более трудные и разнообразные задачи, а так же задачи олимпиадного уровня.

Структура программы концентрическая, т.е. одна и та же тема может изучаться как в 5, так и в 6, 7 классах. Это связано с тем, что на разных ступенях обучения дети могут усваивать один и тот же материал, но уже  разной степени сложности с учетом приобретенных ранее знаний.

Включенные в программу вопросы дают возможность учащимся готовиться к олимпиадам и различным математическим конкурсам. Занятия могут проходить в форме бесед, лекций, экскурсий, игр. Особое внимание уделяется решению задач повышенной сложности.

Задачи факультативного курса по математике определены следующие:

• развитие у учащихся логических способностей;
• формирование пространственного воображения и графической культуры;
• привитие интереса к изучению предмета;
• расширение и углубление знаний по предмету;
• выявление одаренных детей;
• формирование у учащихся таких необходимых для дальнейшей успешной учебы качеств, как упорство в достижении цели, трудолюбие, любознательность, аккуратность, внимательность, чувство ответственности, культура личности;
• адаптация к переходу детей в среднее звено обучения, имеющее профильную направленность.

Для успешного достижения поставленных целей и задач  при формировании групп желательно учитывать не только желание ребенка заниматься, но и его конкретные математические способности. Это можно выявить при беседе с учителем начальной школы, а так же по результатам школьных олимпиад или вводного тестирования за курс начальной школы.  Занятие не должно длиться более 45 минут. Частота занятий – 1 раз в неделю. Программа рассчитана на 35 учебных часа.

Основные цели и задачи курса:

            Цели курса:

• выявление и развитие математических способностей учащихся;

• повышение активности учащихся;

• систематизирование и углубление знаний, совершенствование умений по предложенным темам;

• развитие воображения, математического и логического мышления, памяти, внимания, интуиции детей;

• создание условий для самостоятельной творческой работы учащихся;

• воспитание интереса к математике;

• профессиональная ориентация на профессии, существенным образом связанные с математикой;

Задачи курса:

• развивать познавательную и творческую активность учащихся на основе дифференцированных занимательных заданий;

• обогащать математический язык школьников;

• расширить кругозора учащихся;

• повысить мотивацию обучения для слабоуспевающих школьников;

• развивать коммуникативные навыки в процессе практической и игровой деятельности.

Требования к уровню подготовки учащихся

После изучения данного курса учащиеся должны знать:

• различные системы счисления;
• приёмы рациональных устных и письменных вычислений;
• приёмы решения задач на переливание, движение и взвешивание;

• различные системы мер;
• приёмы решения практических задач на  перегибание, плоские разрезания, делимость.

ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ.

Учащиеся, посещающие факультатив, в конце учебного года должны уметь:

• находить наиболее рациональные способы решения логических задач, используя при решении таблицы и «графы»;
• оценивать логическую правильность рассуждений;
• распознавать плоские геометрические фигуры, уметь применять их свойства при решении различных задач;
• решать простейшие комбинаторные задачи путём систематического перебора возможных вариантов;
• уметь составлять занимательные задачи;
• применять некоторые приёмы быстрых устных вычислений при решении задач;
• применять полученные знания при построениях геометрических фигур и использованием линейки и циркуля;
• применять полученные знания, умения и навыки на уроках математики.

Учебно-тематический план

СОДЕРЖАНИЕ ИЗУЧАЕМОГО КУРСА.

Тема №1. Натуральные числа (18 часов)

Как люди научились считать. Из науки о числах. Из истории развития арифметики. Почему нашу запись называют десятичной. Действия над натуральными числами. Как свойства действий помогают вычислять. Приёмы рациональных вычислений. Отгадывание математических загадок при помощи уравнений. Логические и традиционные головоломки. Задачи на «переливание». Задачи на «взвешивание». Задачи на «движение».

Тема №2. Дробные числа» (17 часов)

Метрическая система мер. Старые русские меры. Как измеряли в древности. Как возникают дроби в практических вычислениях. Задачи на делимость. Перегибания. Плоские разрезания. Математические фокусы. Математические игры. Полушутки. Слишком правильные дроби. Проценты в нашей жизни.

Тема №3 . Итоговое занятие - 1 час

На заключительном занятии учащимся предлагается решение задач международного математического конкурса «Кенгуру».

Методические рекомендации

Основная методическая установка учебного курса «За страницами учебника математики» — обучение школьников навыкам самостоятельной индивидуальной и групповой работы по решению задач различных видов.

Индивидуальное освоение ключевых способов деятельности происходит на основе системы заданий и алгоритмических предписаний, предлагаемых учителем. Кроме индивидуальной, применяется и групповая форма работы.

Учителю необходимо создать условия для реализации ведущей подростковой деятельности — авторского действия, выраженного в практических работах.

Основные типы занятий — лекция и практикум.

В ходе обучения учащимся периодически предлагаются короткие (5— 10 мин) контрольные работы на проверку освоения изученных способов действий. Проводятся кратковременные срезовые работы (тесты, творческая работа) по определению уровня знаний учеников по данной теме. Выполнение контрольных работ способствует быстрой мобилизации и переключению внимания на осмысливание материала изучаемой темы. Кроме того, такая деятельность ведет к закреплению знаний и служит регулярным индикатором успешности образовательного процесса.

Для учащихся на заключительном занятии предлагается решение заданий международного математического конкурса «Кенгуру».

Методическое обеспечение

дополнительной образовательной программы

Формы проведения занятий: урок-обсуждение, деловая игра, практическое занятие, лабораторная работа.

Формы проведения итогов по каждому блоку: консультация, викторина, игра, мини-олимпиада, индивидуальное домашнее задание.

Форма проведения итогового занятия по курсу: игра.

Техническое сопровождение: компьютер, мультимедийный проектор, демонстрационный экран.

Дидактический материал подбирается на основе рекомендуемой ниже литературы.

         В данном разделе рассмотрены три основные темы курса: «Логические задачи», «Знакомство с геометрией», «Занимательное в математике». Указаны разделы по каждой теме с кратким их описанием. Приведены примеры заданий для каждого раздела.

Каждое занятие включает в себя: беседу по данной теме, стихи о математике, занимательные задачи и дидактические игры. Предлагается примерное планирование занятий о старинных системах записи чисел.

Занятие №1.

Тема: «История математики. Старинные системы записи чисел».

Цели: «Познакомить со старинными системами записи чисел. Развивать познавательный интерес к математике, её истории. Развивать память, речь, логическое мышление. Расширять кругозор учащихся, повышать их общую культуру».

Оборудование: таблицы.

Ход занятия.

I.Организация класса.

Речевая разминка.

И прекрасна и сильна

Математики страна

Здесь везде кипит работа,

Все подсчитывают что-то.

Сколько домнам угля надо.

А детишкам шоколада.

Сколько звёзд на небесах,

А веснушек на носах.

II. Сообщение целей факультатива и темы занятия.

III. Изучение нового материала. Старинные системы записи числа.

А) Иероглифическая система древних египтян.

Около 3-2,5 тыс. лет до нашей эры древние египтяне придумали свою числовую систему. В ней ключевые числа: 1, 10, 100 и т.д.- изображались специальными значками- иероглифами. Египтяне высекали их на стенах погребальных камер, писали тростниковым пером на свитках папируса.

Для записи чисел они употребляли следующие иероглифы:

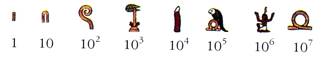
Б) Римские цифры.

Среди множества иероглифических систем счисления, которые существовали в разные времена у разных народов, только одна используется до сих пор. Эти цифры встречаются на циферблатах часов, фронтонах старинных и современных зданий, памятниках, страницах книг. Речь идет о римской системе счисления.

Физкультминутка.

IV. Занимательные задачи.

А) Снежный барс- отличный охотник. На охоте он не уступает в ловкости льву. Сравни массу барса и льва, если известно, что масса снежного барса достигает 40кг, а льва- 2ц. (1ц = 100 кг).

Б) Маленькая мышка, живущая под  корнями деревьев, делает запасы на зиму. В норке одной мышки было найдено 5 кг семян. Сколько кг семян перетащат в свои норки 2,3, и т. д. мышки.

V. Игра «Гномик, который любит таблицу умножения».

VI.Итоги.

Занятие №2.

Тема: « История математики. Римские цифры. Алфавитные системы».

Цели: «Познакомить с римскими цифрами и алфавитными системами. Развивать познавательный интерес к математике, её истории. Развивать память, мышление и речь».

Оборудование: таблицы, иллюстрирующие обозначение чисел римскими цифрами и алфавитные системы.

Ход занятия.

I.Организация класса.

Речевая гимнастика.

II. Римские цифры.

Римским цифрам около 2,5 тыс. лет. Как читать римские цифры? Правило записи римских чисел гласит: « Если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей, то меньшая вычитается из большей». В наши дни любую из римских цифр запрещается записывать в одном числе более трёх раз подряд. ( V1111)

Эта таблица позволяет обозначить любое число от 1 до 3999. Вот как будет выглядеть число 3999- МММСМХС1Х.

У многих народов для обозначения числа 1 применялся один и тот же символ- вертикальная чёрточка. Это самое древнее число в истории человечества. Оно возникло из простой черты на земле, из зарубки на дереве или кости.

III. Алфавитные системы.

В древности широко применялись системы, в которых числа обозначались буквами. Для обозначения чисел над буквами сверху ставили специальный значок- титло (~).

С помощью этой таблицы можно легко записать любое целое число от 1 до 999 включительно, например.

 77- ЗО, 288- СПИ, 498- УЧИ.

IV. Игра. ЭВМ.

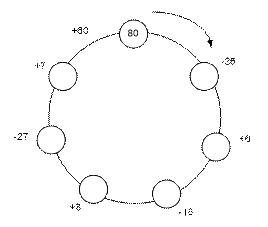
V. Итоги.

Занятие № 3.

Тема: « Из истории больших чисел. Числа- великаны».

Цели: «Познакомить с числами – великанами. Расширить кругозор учащихся. Путём заучивания стихотворений развивать память. Решая нестандартные задачи развивать логическое мышление. Воспитывать интерес к математике».

Оборудование: таблица чисел- великанов, игра.

Ход занятия.

 I. Организация класса.

II. Речевая гимнастика.

III. Чтение и заучивание стихотворения.

Давайте, ребята, учиться считать:

Делить, умножать, прибавлять, вычитать.

Запомните все, что без точного счёта

Не сдвинется с места любая работа.

Без счёта не будет на улице света.

Без счёта не может подняться ракета.

Без счёта письмо не найдёт адресата

И в прятки сыграть не сумеют ребята.

Считайте, ребята, точнее считайте,

Хорошее дело смелей прибавляйте,

Плохие дела поскорей вычитайте.

IV. Изучение нового материала.

Число 2 немец произнесёт как « цвай», англичанин «ту». А вот число 1 000 000 и на русский и немец, и англичанин назовут одинаково ­– миллион. В 1271г. венецианский

купец Марко Поло отправился в далёкий и загадочный Китай. Путь в Китай лежал через многие страны. Вернувшись домой через четверть века, он не переставал восторгаться увиденными чудесами. В его речи то и дело слышалось: « Миллионе…Миллионе». Слово « mille» ( тысяча). Тысяча, тысяч.

1 000 000 000-миллиард, биллион.

1 000 000 000 000-триллион.

1 000 000 000 000 000-квадриллион.

1 000 000 000 000 000 000-квинтиллон.

1 000 000 000 000 000 000 000-секстиллион.

1 000 000 000 000 000 000 000 000-септилион.

1 000 000 000 000 000 000 000 000-октиллион.

V. Занимательные задачи.

1.Два сына и два отца съели три яйца. По сколько яиц съел каждый? (По одному т. к. один из них является одновременно и отцом своего ребёнка и сыном своего отца.)

2.Шёл турист в Москву, а навстречу ему три грибника, у каждого по две корзины. Сколько человек шло в Москву?

3.Что легче один килограмм ваты или один килограмм железа?

VI. Игра-соревнование. Кто быстрее долетит до Марса.

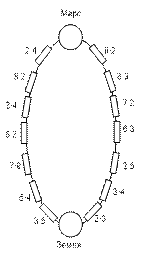
VII. Итоги.

Занятие № 4.

Тема: «Четыре действия арифметики. Сложение и вычитание. Возникновение действий «+» и «­­­­–».

Цели: «Познакомить учащихся с историей появления знаков «+» и «–». Развивать память и логическое мышление. Воспитывать интерес к математике».

Оборудование: игра, занимательные задачи.

Ход занятия.

I. Организация класса.

II. Речевая гимнастика. Стихотворение. «Давайте, ребята, учиться считать».

III. Изучение нового материала.

Заглянем на страницы истории. Знаки «+» и «–» широко применялись в торговой практике. Купцы торговали вином, на пустых бочках ставили символ «–», означавший убыль. Если бочку заполняли  вином, то символ «-.» перечёркивали и получался таким образом символ «+» , означавший прибыль. Символы «+» и «–» как математические знаки для операции сложения и вычитания ввёл в XV веке математик Видман. До появления знака «+» писали: 3 и 6, 4 и 5. Впоследствии действие сложения стали записывать с помощью знака «+»: 3+6, 4+5. Знаками «+» и «–» пользуются и по сей день.

IV. Занимательные задачи.

1.Два мальчика вместе шли в школу и на дороге нашли десять рублей. Сколько денег найдут пять ребят. (Нисколько).

2. На столе 4 стакана с ягодами. Вова съел один стакан ягод. Сколько стаканов осталось на столе? (Четыре. Вова же съел ягоды, а не стакан.)

3. У стены стоит кадушка, а в кадушке той лягушка. Если б было семь кадушек, сколько было бы лягушек? (Одна, которая сидит в кадушке, в остальных может не быть ни одной.)

4. Росли 4 березы, на каждой березе – по 4 больших ветке, на каждой большой ветке – по 4 маленьких, на каждой маленькой – по 4 яблока. Сколько всего яблок? (На березе яблоки не растут)

V. Игра. «Гномик».

VI. Итоги.

Занятие № 5.

Тема: « Четыре действия арифметики. Умножение и деление».

Цели: «Познакомить учащихся с историей появления знаков «*» и «:».Развивать мышление, память и речь».

Оборудование: таблицы, стихотворение, игра.

Ход занятия.

I.Организация класса.

II.Речевая гимнастика.

III.Чтение и заучивание стихотворений.

IV.Изучение нового материала.

Умножение чисел сейчас изучают в начальной школе. А вот в средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет. За тысячелетия развития математики было придумано множество способов умножения чисел. Один из способов носит название решётчатое умножение.

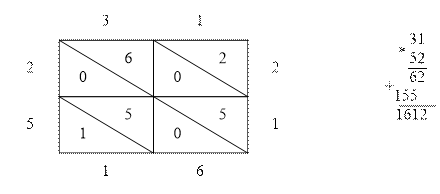
Хотя умножение в старину и считалось нелёгким делом, однако деление было ещё сложнее. В средние века людей, умевших производить деление, можно было пересчитать чуть ли не по пальцам. Их уважительно называли магистрами деления. Они переезжали из города в город по приглашениям купцов, желавших привести в порядок свои счета.

Занимательная задача.

         Один старик оставил своим 3 сыновьям 19 верблюдов. Старшему сыну половину, среднему- 4 часть, младшему- пятую. Братья обратились к мудрецу. 19- не делится ни на 2, ни на 4, ни на 5. Можешь ли ты помочь нашему горю. –Нет ничего проще- возьмите моего верблюда. Братья дома разделили 20:2, 20:4,20:5. 10+5+4=19. При этом 1 верблюд остался. Раздосадованные братья вернулись к мудрецу и пожаловались.

Это не лишний – это мой верблюд.

V.Задание на развитие памяти.

Я показываю ряд цифр, их надо запомнить.

2, 3, 5, 7,3,5,7.

VI.Игра «Математический футбол».

VII. Итоги.

Занятие №6.

Тема: «Открытие нуля». 

Цели: «Познакомить с историей открытия нуля. Развивать память, мышление и речь. Воспитывать интерес к математике».

Оборудование: стихи, игра.

Ход занятия.

I.Организация класса.

II.Речевая гимнастика.

III. Чтение и разучивание стихотворение о нуле.

Сказал весёлый, круглый ноль

Соседке единице:

- С тобою рядышком позволь

Стоять мне на странице!

Она окинула его

Сердитым, гордым взглядом:

- Ты, ноль, не стоишь ничего,

Не стой со мною рядом!

Ответил ноль:

- Я признаю,

Что ничего не стою,

Но можешь стать ты десятью,

Коль буду я с тобою.

Так одинока ты сейчас,

Мала и худощава,

Но будешь больше в десять раз,

Когда я стану справа!

Напрасно думают, что ноль

Играет маленькую роль.

Мы двойку в двадцать превратим

Из троек и четвёрок

Мы можем, если захотим,

Составить тридцать, сорок

Пусть говорят, что мы ничто

С двумя нолями вместе

Из единицы выйдет сто.

Из двойки целых двести.

                               С. Я. Маршак.

IV.Изучение нового материала.

История нуля берёт своё начало с незапамятных времён. Впервые нуль появился примерно две тысячи лет назад. В древности индейцы вместо нуля говорили «пусто» и при записи ставили точку. Позднее вместо точки стали рисовать кружок. Такой кружок назывался «сунья», что значит «пустое место». Арабские математики перевели слово «сунья» по смыслу на свой язык: стали говорить «сифр». А это уже знакомое нам слово цифра. Оно досталось нам по наследству от арабов. Знаки для обозначении чисел, которыми мы пользуемся называют цифрами. Их десять: 0, 1, 2, 3,4,5,6,7,8,9. У нуля были и другие названия- «ничто», «низачто», «оном» ( за сходство с буквой О). Древние люди нуль применяли лишь для обозначения пропущенных разрядов. Писать нули в конце записи числа, они не догадывались. В настоящее время с нулём знакомятся в 1 классе и люди не замечают, что открытие нуля- одно из величайших событий в математике.

V.  Занимательные задачи.

1.Что случилось в Москве 31 февраля 2006 года

2.Какой год продолжается один день?  (Новый год).

3.Укого есть шапка без головы, нога без сапога?  (У гриба).

VI. Игра. Математическая цепочка.

VII. Итоги.

Занятие № 7.

Тема: «История линейки».

Цели: «Познакомить учащихся с историей линейки в России. Развивать память, мышление и речь. Воспитывать интерес к математике».

Оборудование: занимательные задачи, загадки.

Ход занятия.

I. Организация класса.

II. Речевая гимнастика.

Чтение стихотворений о математике.

III. Беседа по теме.

Знаете ли вы, что 1989 г.у линейки был юбилей. Ей исполнилось 2000 лет. Однако линейкой пользовались и в более поздние времена. В средневековье, например, немецкие монахи для разметки линий на листах пергамента (так называлась бумага) пользовались тонкими свинцовыми пластинками. А в ряде стран Европы, в том числе и в Древней Руси, для этих целей применяли железные прутья. В летописях их называли «шильцами». Когда в 1789г.во Франции началась работа по внедрению метрической системы мер, в Париже были изготовлены две платиновые линейки с метрическими делениями длиной в 1м и шириной 25мм,называемые эталоном метра. По их образцу изготовили деревянные линейки для академиков. А позднее и для парижских студентов. У школьников линейки появились только в конце 19 века. В Россию линейка попала в 1812г.в качестве военного трофея. В 1899г. по инициативе знаменитого химика Д.И.Менделеева приступили к производству линейки в России- так в нашей стране началось постепенное внедрение метрической системы мер.

IV. Занимательные задачи.

1. Чтобы поужинать, волку достаточно 2кг мяса, но если он голоден то может съесть в 5 раз больше. Сколько мяса может съесть годный волк.

2.Сколько мёда могут собрать пчёлы с 3га гречичного поля, если с 1га они собирают 70кг мёда?

V. Загадки.

1. Без ног и без крыльев оно

    Быстро летит, не догонишь его. (Время).

2.Под Новый год пришёл он в дом

    Таким румяным толстяком

    Но с каждым днём терял он вес

    И наконец совсем исчез. (Календарь).

3.Вышел старик- годовик

   Махнул рукавом,

И полетели двенадцать птиц,

У каждой птицы по четыре крыла,

В каждом крыле по семь перьев,

Каждое перо с одной стороны чёрное

А с другой белое. (Год, месяцы, недели, дни, ночи.)

VI.Игра.

Один из величайших греческих математиков древности Пифагор (580- 500г. до нашей эры) считал, что числа очень важны для жизни людей. Попробуйте сами прочитать, что он говорил о числах.

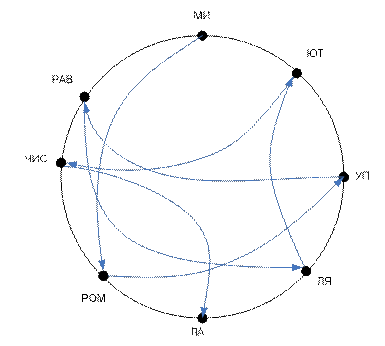
Занятие № 8.

ТЕМА: «ЛОГИЧЕСКИЕ  ЗАДАЧИ»

1. Задачи на переливание.

Рассматриваются задачи, подобные данной: «Как с помощью двух ведер по 2 л и 7 л можно набрать из реки ровно 3 л воды?».

Задачи на переливание представляют собой такие задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости.

При решении таких задач необходимо учитывать следующие замечания:

разрешается наливать в сосуд ровно столько жидкости, сколько в нем помещается;

 разрешается переливать всю жидкость из одного сосуда в другой, если она в него вся помещается;

 разрешается отливать из одного сосуда в другой столько жидкости, сколько необходимо, чтобы второй сосуд стал полным.

5.1 Как, имея 2 ведра емкостями 4л и 9л, налить из водопроводного крана 6л воды?

5.2 В первый сосуд входит 8л, и он наполнен водой. Имеется ещё 2 пустых сосуда емкостями 5л и 3л. Как с помощью этих сосудов отмерить ровно 1 л?

5.3 В первый сосуд входит 12 л, и он наполнен водой. Имеется ещё 2 пустых сосуда емкостями 5л и 8л. Как разделить воду на две равные части?

5.4 Имеется 2 типа песочных часов: одни отмеряют 7 мин, а другие – 11 мин. Как с их помощью отмерить 15 мин, необходимых для того, чтобы сварить вкрутую яйцо?

5.5 В бочке 28л бензина. Имеется 2 ведра емкостью по 7л, в которые нужно налить по 6л бензина. Кроме того, есть черпак емкостью 4л. Как можно осуществить разлив?

5.6 В бочке хранится несколько вёдер бензина. Как из неё отлить 6л бензина в другую бочку с помощью 9- и 5-литрового бидонов?

5.7 Имеется 2 сосуда емкостями 2л и 5л. Нужно, пользуясь этими сосудами, получить 1л воды из водопроводного крана.

5.8 Однажды мачеха дала Золушке два ведра объемами 5 и 9 литров и сказала ей принести из колодца ровно 3 литра воды. Золушка справилась с задачей. А Вы смогли бы? Покажите как.

5.9 Имеются три сосуда вместимостью 8, 5 и 3 литра. Наибольший сосуд полон молока. Как разделить это молоко на две равные части, используя остальные сосуды?

Задачи решаются в два способа с обязательным оформлением в таблице. Уровень сложности зависит от количества ходов-переливаний.

Занятие № 9.

2. Задачи на взвешивание.

Рассматриваются задачи, подобные данной: «Как с помощью весов без гирь можно ровно за два взвешивания отделить из девяти одинаковых монет одну фальшивую, которая легче по весу?».

Решение рассматривается в виде «дерева» ходов.

Занятие № 10.

3. Логические задачи, решаемые с помощью таблиц.

1. Пример задачи:

"В одном дворе живут четыре  друга. Вадим и шофер старше Сергея; Николай и слесарь занимаются боксом; электрик – младший из друзей; по вечерам Антон и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей".

Решение оформляется в виде таблиц, где знаком «+» отмечается возможная, реальная ситуация, а знаком «-» - невозможная по условию задачи. Сложность варьируется от 3-х элементов сравнивания (более простые задачи) до 5-ти (более сложные).

Занятие № 11.

4. Задачи на делимость чисел.

Используя признаки делимости на 2; 3; 4; 5; 9; 10 и т.д. решаются задачи, подобные данной: «Можно ли разделить на 3 одинаковых букета 21 розу и 17 гвоздик, чтобы в каждом букете были и розы, и гвоздики?».

Задачи не очень трудные для детей, поэтому их решение не обязательно записывать, можно ограничиться устным подробным ответом.

Занятие № 12.

5. Задачи на принцип Дирихле.

         Известные в математике задачи про кроликов и кур. «На дворе гуляли кролики и куры. Всего 40 ног и 16 голов. Сколько было кроликов и сколько кур?».

         При решении подобных задач необходимо, чтобы дети попытались запомнить алгоритм выполнения действий. Во-первых, надо «поставить» кроликов на 2 лапы и понять, что на земле и у кроликов, и у кур стоит по одинаковому числу ног. Во-вторых, понять, что на каждую голову теперь приходится по 2 ноги на полу, затем из общего количества ног по условию задачи вычесть те, которые на полу – узнаем, сколько поднятых. Но подняли-то по 2 лапки кролики. Значит, узнаем ответ на вопрос задачи.

Занятие № 13.

6. Комбинаторные задачи.

Основной принцип комбинаторики: «Если одно действие можно выполнить k способами, другое – m способами, а третье – n способами, то все три действия можно выполнить k·m·n способами».

К выводу этого принципа приходим опытным путем, решая задачи на 2 или 3 действия с помощью «дерева».  Затем подобные задачи уже решаются быстрее в одно действие. Закон распространяется на 2 и более действий.

Задача: «Сколько 3-х-значных четных чисел можно составить из цифр 0; 1; 2; 3; 4; 5?».

Занятие № 14.

8. Задачи, решаемые с помощью графов.

Пример задачи: У трех подружек – Ксюши, Насти и Оли – новогодние карнавальные костюмы и шапочки к ним белого, синего и фиолетового цветов. У Насти цвет костюма и шапочки совпали, у Ксюши ни костюм, ни шапочка не были фиолетового цвета, а Оля была в белой шапочке, но цвет костюма у неё не был белым. Как были одеты девочки?

Занятие № 15.

9.Игровые задачи.

К ним относятся задачи; «Как, не отрывая карандаш от бумаги, обвести фигуру так, что бы не проходить по одному месту дважды?». Возможны задачи на раскраски, последовательное соединение точек.

Занятие № 16.

ТЕМА: «ЗНАКОМСТВО С ГЕОМЕТРИЕЙ»

Все занятия носят практический и игровой характер.

1. Простейшие геометрические фигуры (круг, треугольник, квадрат, прямоугольник, ромб, параллелограмм, трапеция), их свойства.

         Даются определения фигур, рассматриваются «видимые» свойства.

         Круг, его радиус, диаметр, хорда.

         Треугольник. Виды треугольников. Равнобедренный треугольник. Равносторонний треугольник. Прямоугольный треугольник, его элементы, египетский треугольник.

Занятие № 17.

2. Задачи на разрезание.

         Одни из самых сложных задач. Разрезать фигуру на требуемое число частей так, чтобы из них можно было составить другую заданную фигуру. Можно использовать игру-головоломку «Танграм».

Занятие № 18.

3. Геометрические головоломки со спичками.

         Проводится под девизом «Спички детям - не игрушка!». Если есть такая возможность, то у каждого ребенка на столе вместо спичек – счетные палочки. Выкладывая из них заданную фигуру, он с помощью заданного количества перемещений палочек должен получить другую фигуру.

Занятие № 19.

4. Закончить рисунок по образцу.

Рисунок выполняется простым карандашом по линейке в формате 10х10 клеток обычного тетрадного листа по принципу раскраски в шахматном порядке. Пример готового рисунка

Занятие № 20.

ТЕМА: «ЗАНИМАТЕЛЬНОЕ В МАТЕМАТИКЕ»

Все занятия проводятся в игровой форме.

1. «Магические» фигуры.

         Знакомство с «магическими квадратами», историческая справка. Построение квадратов 3х3; 5х5. Принцип быстрого построения таких квадратов.

Занятие № 21.

2. Ребусы, головоломки, кроссворды.

         Для разгрузки используются почти всегда. Берутся из разнообразных источников, дети могут сами их приносить. Обучение разгадыванию простейших японских числовых кроссвордов.

Занятие № 22.

3. Математические фокусы и софизмы.

         Так же используются для разрядки. Например: «Задумайте число, умножьте его на… и т. д. Назовите свой результат и я отвечу, какое число вы задумали.»

Занятие № 23.

4. Занимательный счет.

Приемы быстрого сложения, вычитания, умножения, деления и возведения в квадрат. Например, умножение на 4, на 10, на 11, на 25 и др. Использование сочетательного свойства сложения и  распределительного свойства умножения, выбор удобного порядка действий.

Занятие № 24.

5. Математические игры.

Многие занимательные игры основаны на свойствах чисел, которые не изучают в школе. Рассматриваются такие игры, как "Битва чисел", "Ним", например: На столе лежат три кучки камешков. В одной кучке один камешек, в другой – два, в третьей – три. Двое играющих берут поочередно камешки, причем за один раз можно взять любое число камешков из одной кучки. Выигрывает тот, кто берет последний камешек. Докажите, что начинающий игру наверняка проиграет. "Игра в 15", знакомство с кубиком Рубика, ханойской башней и т.п., "Математика и шифры".

Занятие № 25-33.Практические уроки.

КОНТРОЛЬ ОЖИДАЕМЫХ РЕЗУЛЬТАТОВ.

Контроль осуществляется, в основном, при проведении контрольных работ по темам.  Ниже приведена примерная итоговая работа, которая носит рекомендательный характер. Учитель вправе изменить содержание, уровень сложности, количество и тематику задач или провести математический праз-дник.

Занятие № 35.          

                           Итоговая контрольная работа.

1.    Когда Даша, Таня и Люда спросили, какие оценки им поставили за конт-рольную работу, учительница сказала: «В вашем классе двоек вообще нет, а у вас оценки разные, причем у Даши - не 3, у Люды – не 3 и не 5. Какую оценку получила каждая девочка?

2. Если бы завтрашний день был вчерашним, то до воскресенья оставалось бы столько дней, сколько дней прошло от воскресенья до вчерашнего дня. Какой сегодня день?
3. У деда 2 бидона емкостью 2 и 7 литров. Помоги ему набрать из речки 3 литра воды. Расскажи, как это сделать.
4. Во дворе гуляли куры и собачки. Мальчик подсчитал их лапы – получилось 10. Скажи, сколько могло быть кур и сколько собак?
5. В бутылке, стакане, кувшине и банке налиты молоко, лимонад, квас и вода. Известно, что вода и молоко находятся не в бутылке, в банке – не лимонад и не вода, а сосуд с лимонадом стоит между кувшином и сосудом с квасом. Стакан стоит около банки и сосуда с молоком. Определите, в каком сосуде какая жидкость.
6. Сколько существует трехзначных чисел, все цифры которых – нечетные и никакие не повторяются внутри одного числа?
7. Из 15 котят 8 рыжих и 7 пушистых, и других нет. Есть ли среди этих котят хоть один рыжий и пушистый одновременно?

ЛИТЕРАТУРА:

1. И.Я. Депман, Н.Я. Виленкин. «За страницами учебника математики: Пособие для учащихся 5 – 6 классов сред школ. – М.: «Просвещение», 1989 г.

2. «Все задачи "Кенгуру"», С-П.,2003г.

3. Л.М.Лихтарников. «Занимательные задачи по математике», М.,1996г.

4. Е.В.Галкин. «Нестандартные задачи по математике», М., 1996г.

5. А.Я.Кононов. «Математическая мозаика», М., 2004 г.

6. Б.П.Гейдман. «Подготовка к математической олимпиаде», М., 2007 г.

7. Т.Д.Гаврилова. «Занимательная математика», изд. Учитель, 2005 г.

8. Е.В.Галкин. «Нестандартные задачи по математике, 5-11 классы», М.,  1969 г.

9. «Ума палата» - игры, головоломки, загадки, лабиринты. М., 1996г.

10. Е.Г.Козлова. «Сказки и подсказки», М., 1995г.

11. И.В.Ященко «Приглашение на математический праздник». М., МЦНПО, 2005г.

12. А.С.Чесноков, С.И.Шварцбурд, В.Д.Головина, И.И.Крючкова, Л.А.Литвачук. «Внеклассная работа по математике в 4 – 5 классах». / под ред. С.И.Шварцбурда. М.: «Провсещение», 1974 г.

13. А.  Я.Котов. «Вечера занимательной арифметики»

14. Ф.Ф.Нагибин. «Математическая шкатулка». М.: УЧПЕДГИЗ, 1961 г.

15. В.Н.Русанов. Математические олимпиады младших школьников. М.: «Просвещение», 1990 г.

16. С.Н.Олехник, Ю.В.Нестеренко, М.К.Потапов. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985 г.

 17. Е.И.Игнатьев. Математическая смекалка. Занимательные задачи, игры, фокусы, парадоксы. – М., Омега, 1994 г.